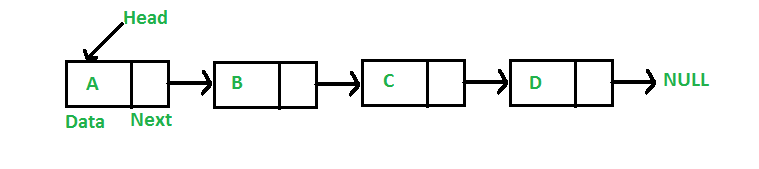
Linked List | Set 1 (Introduction)
Like arrays, Linked List is a linear data structure. Unlike arrays, linked list elements are not stored at a contiguous location; the elements are linked using pointers.
Why Linked List?
Arrays can be used to store linear data of similar types, but arrays have the following limitations.
1) The size of the arrays is fixed: So we must know the upper limit on the number of elements in advance. Also, generally, the allocated memory is equal to the upper limit irrespective of the usage.
2) Inserting a new element in an array of elements is expensive because the room has to be created for the new elements and to create room existing elements have to be shifted.
Arrays can be used to store linear data of similar types, but arrays have the following limitations.
1) The size of the arrays is fixed: So we must know the upper limit on the number of elements in advance. Also, generally, the allocated memory is equal to the upper limit irrespective of the usage.
2) Inserting a new element in an array of elements is expensive because the room has to be created for the new elements and to create room existing elements have to be shifted.
Linked List | Set 2 (Inserting a node)
We also created a simple linked list with 3 nodes and discussed linked list traversal.
All programs discussed in this post consider following representations of linked list
In this post, methods to insert a new node in linked list are discussed. A node can be added in three ways
1) At the front of the linked list
2) After a given node.
3) At the end of the linked list.
1) At the front of the linked list
2) After a given node.
3) At the end of the linked list.
Add a node at the front: ( 4 steps process)
The new node is always added before the head of the given Linked List. And newly added node becomes the new head of the Linked List. For example if the given Linked List is 10->15->20->25 and we add an item 5 at the front, then the Linked List becomes 5->10->15->20->25. Let us call the function that adds at the front of the list is push(). The push() must receive a pointer to the head pointer, because push must change the head pointer to point to the new node (See this)
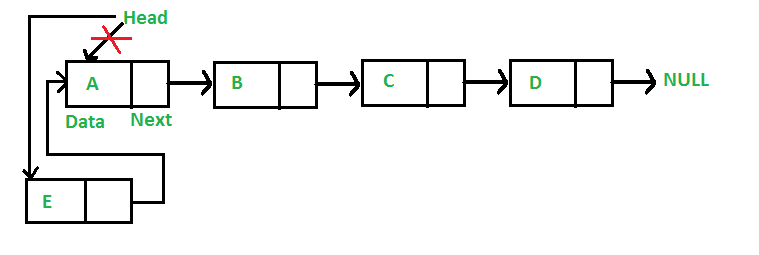
The new node is always added before the head of the given Linked List. And newly added node becomes the new head of the Linked List. For example if the given Linked List is 10->15->20->25 and we add an item 5 at the front, then the Linked List becomes 5->10->15->20->25. Let us call the function that adds at the front of the list is push(). The push() must receive a pointer to the head pointer, because push must change the head pointer to point to the new node (See this)

Following are the 4 steps to add node at the front.
Add a node after a given node: (5 steps process)
We are given pointer to a node, and the new node is inserted after the given node.
We are given pointer to a node, and the new node is inserted after the given node.
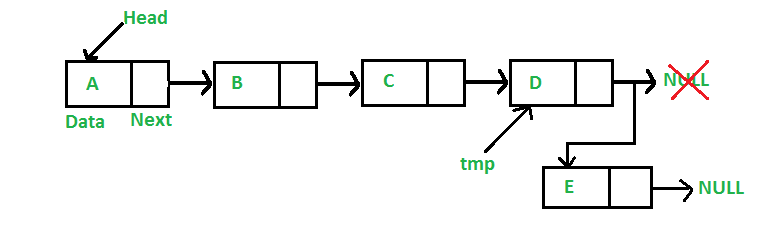
Add a node at the end: (6 steps process)
The new node is always added after the last node of the given Linked List. For example if the given Linked List is 5->10->15->20->25 and we add an item 30 at the end, then the Linked List becomes 5->10->15->20->25->30.
Since a Linked List is typically represented by the head of it, we have to traverse the list till end and then change the next of last node to new node.
The new node is always added after the last node of the given Linked List. For example if the given Linked List is 5->10->15->20->25 and we add an item 30 at the end, then the Linked List becomes 5->10->15->20->25->30.
Since a Linked List is typically represented by the head of it, we have to traverse the list till end and then change the next of last node to new node.
Linked List | Set 3 (Deleting a node)
e have discussed Linked List Introduction and Linked List Insertion in previous posts on singly linked list.
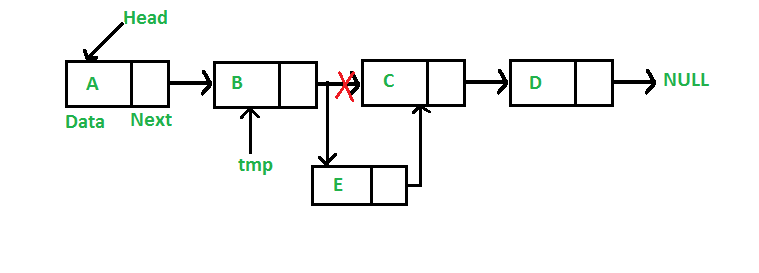
Let us formulate the problem statement to understand the deletion process. Given a ‘key’, delete the first occurrence of this key in linked list.
To delete a node from linked list, we need to do following steps.
1) Find previous node of the node to be deleted.
2) Change the next of previous node.
3) Free memory for the node to be deleted.
To delete a node from linked list, we need to do following steps.
1) Find previous node of the node to be deleted.
2) Change the next of previous node.
3) Free memory for the node to be deleted.
Circular Linked List | Set 1 (Introduction)
Circular linked list is a linked list where all nodes are connected to form a circle. There is no NULL at the end. A circular linked list can be a singly circular linked list or doubly circular linked list.

Advantages of Circular Linked Lists:
1) Any node can be a starting point. We can traverse the whole list by starting from any point. We just need to stop when the first visited node is visited again.
1) Any node can be a starting point. We can traverse the whole list by starting from any point. We just need to stop when the first visited node is visited again.
2) Useful for implementation of queue. Unlike this implementation, we don’t need to maintain two pointers for front and rear if we use circular linked list. We can maintain a pointer to the last inserted node and front can always be obtained as next of last.
3) Circular lists are useful in applications to repeatedly go around the list. For example, when multiple applications are running on a PC, it is common for the operating system to put the running applications on a list and then to cycle through them, giving each of them a slice of time to execute, and then making them wait while the CPU is given to another application. It is convenient for the operating system to use a circular list so that when it reaches the end of the list it can cycle around to the front of the list.
4) Circular Doubly Linked Lists are used for implementation of advanced data structures like Fibonacci Heap.
Why Circular? In a singly linked list, for accessing any node of linked list, we start traversing from the first node. If we are at any node in the middle of the list, then it is not possible to access nodes that precede the given node. This problem can be solved by slightly altering the structure of singly linked list. In a singly linked list, next part (pointer to next node) is NULL, if we utilize this link to point to the first node then we can reach preceding nodes. Refer this for more advantages of circular linked lists.
The structure thus formed is circular singly linked list look like this:
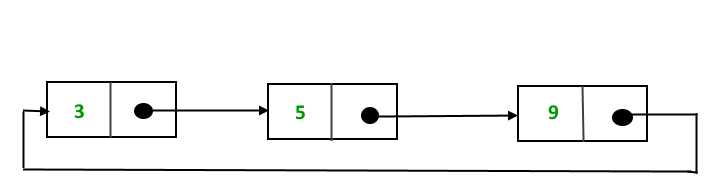

In this post, implementation and insertion of a node in a Circular Linked List using singly linked list are explained.
Implementation
To implement a circular singly linked list, we take an external pointer that points to the last node of the list. If we have a pointer last pointing to the last node, then last -> next will point to the first node.
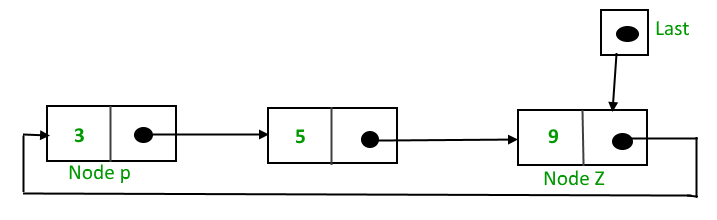
The ponter last points to node Z and last -> next points to node P.
To implement a circular singly linked list, we take an external pointer that points to the last node of the list. If we have a pointer last pointing to the last node, then last -> next will point to the first node.

The ponter last points to node Z and last -> next points to node P.
Why have we taken a pointer that points to the last node instead of first node ?
For insertion of node in the beginning we need traverse the whole list. Also, for insertion and the end, the whole list has to be traversed. If instead of start pointer we take a pointer to the last node then in both the cases there won’t be any need to traverse the whole list. So insertion in the begging or at the end takes constant time irrespective of the length of the list.
For insertion of node in the beginning we need traverse the whole list. Also, for insertion and the end, the whole list has to be traversed. If instead of start pointer we take a pointer to the last node then in both the cases there won’t be any need to traverse the whole list. So insertion in the begging or at the end takes constant time irrespective of the length of the list.
Circular Singly Linked List | Insertion
Insertion
A node can be added in three ways:
A node can be added in three ways:
- Insertion in an empty list
- Insertion at the beginning of the list
- Insertion at the end of the list
- Insertion in between the nodes
Insertion in an empty List
Initially when the list is empty, last pointer will be NULL.

After inserting a node T,
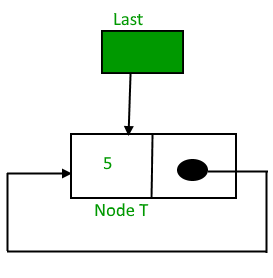
After insertion, T is the last node so pointer last points to node T. And Node T is first and last node, so T is pointing to itself.
Function to insert node in an empty List,
insertion at the beginning of the list
To Insert a node at the beginning of the list, follow these step:
1. Create a node, say T.
2. Make T -> next = last -> next.
3. last -> next = T.
After insertion,
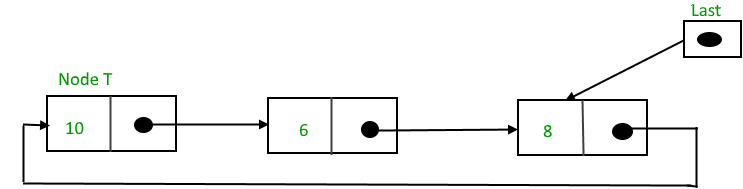
Function to insert node in the beginning of the List,
To Insert a node at the beginning of the list, follow these step:
1. Create a node, say T.
2. Make T -> next = last -> next.
3. last -> next = T.

After insertion,

Function to insert node in the beginning of the List,
Insertion at the end of the list
To Insert a node at the end of the list, follow these step:
1. Create a node, say T.
2. Make T -> next = last -> next;
3. last -> next = T.
4. last = T.
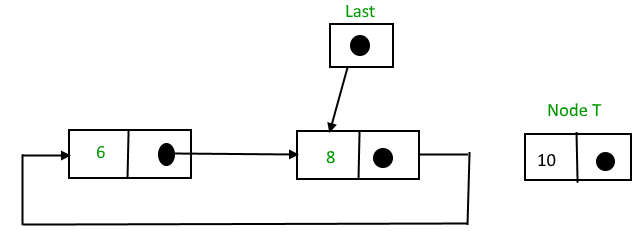
After insertion,
Function to insert node in the end of the List,
To Insert a node at the end of the list, follow these step:
1. Create a node, say T.
2. Make T -> next = last -> next;
3. last -> next = T.
4. last = T.

After insertion,

Function to insert node in the end of the List,
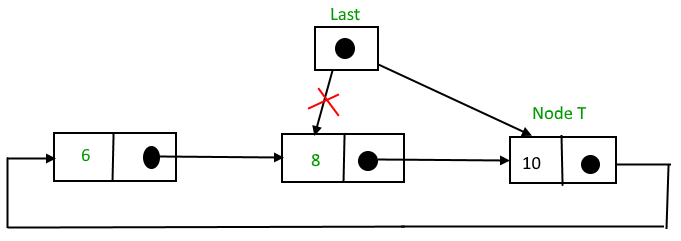
Insertion in between the nodes
To Insert a node at the end of the list, follow these step:
1. Create a node, say T.
2. Search the node after which T need to be insert, say that node be P.
3. Make T -> next = P -> next;
4. P -> next = T.
To Insert a node at the end of the list, follow these step:
1. Create a node, say T.
2. Search the node after which T need to be insert, say that node be P.
3. Make T -> next = P -> next;
4. P -> next = T.
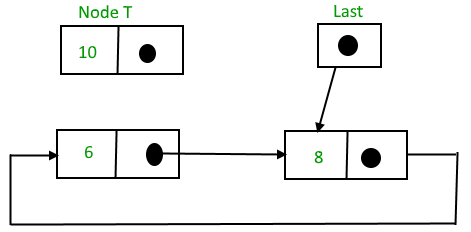
Suppose 12 need to be insert after node having value 10,
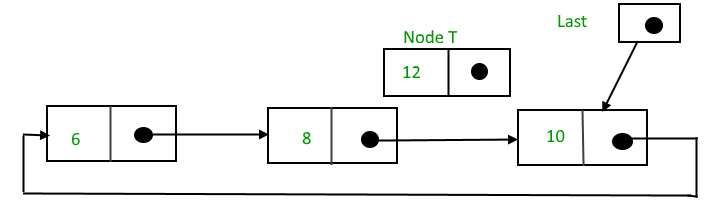
After searching and insertion,
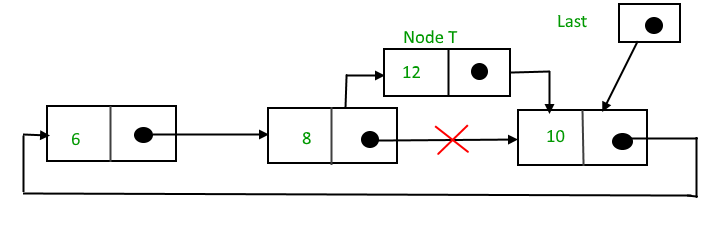
Function to insert node in the end of the List,

After searching and insertion,

Function to insert node in the end of the List,
Following is a complete program that uses all of the above methods to create a circular singly linked list.
Circular Singly Linked List | deletion
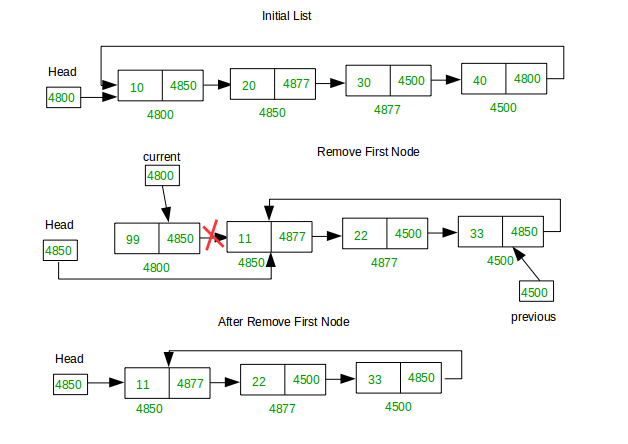
1. First position
We have a list of nodes and we're trying to delete the head of the list. 4800 was the head of the list before we delete it and now 4850 becomes the head of the list.
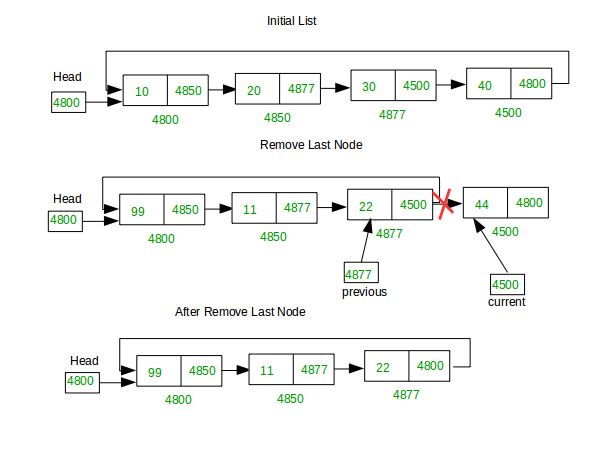
2. Last position
Now we're going to delete the tail of the list. In this case we're deleting 4500 from (4800-4850-4877-4500) and now the list becomes (4800-4850-4877).
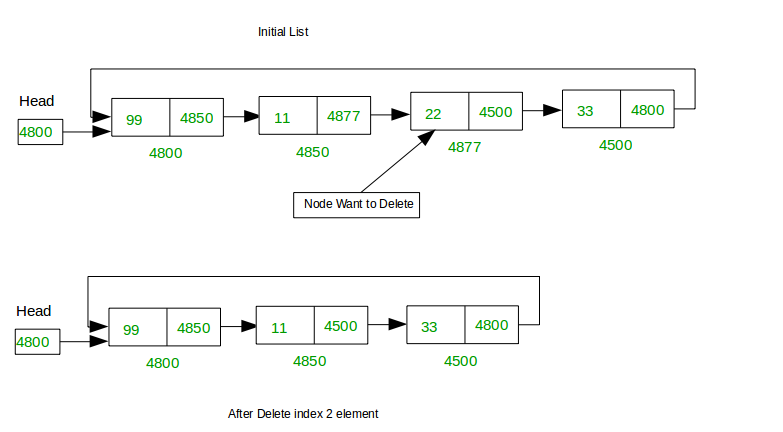
3. Any given position
We have a list (4800-48650-4877-4500). Now we're going to delete a node from any given position but in this case we're going to delete 4877 from the list and now the list becomes (4800-4850-4500).
Doubly Linked List | Introduction
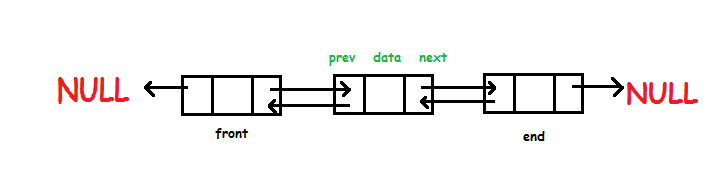
Double Linked List are a linked list where it has two references called next and previous. It's different from Singly Linked List because it can transverse two ways inside the list. It's easier to perform a deletion in Double Linked List.
Doubly Linked List | Insertion
1. At the front of the Doubly Linked List
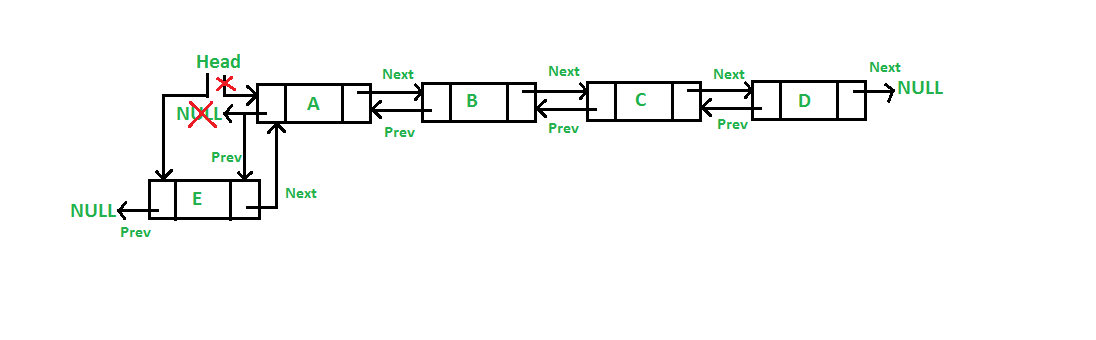
We're going to add a new node in front of the head of the given list. After we add it, it becomes the new head of the list. In this case A is the head of the list A-B-C-D then we add E as the new head of the list and the list becomes E-A-B-C-D.
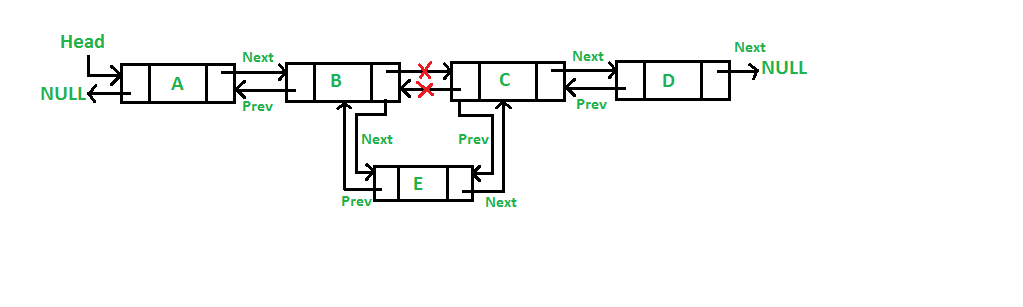
2. After a given node
We're going to add a new node E to the list A-B-C-D. In this case E is added in between B and C. Therefore the list becomes A-B-E-C-D
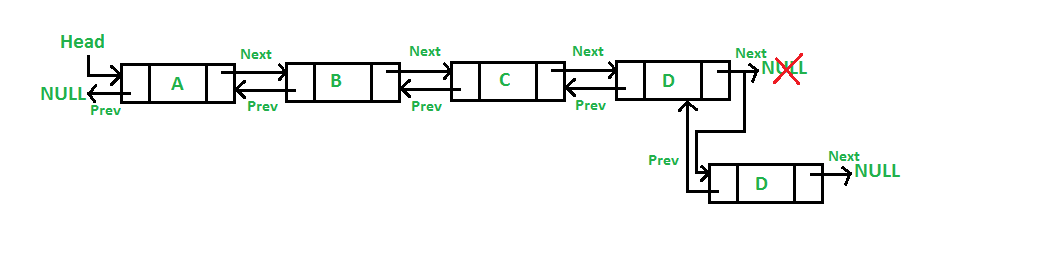
3. At the end of Doubly Linked List
It works the same way as we insert a new node at the front of The Double Linked List but now we're going to insert a new node at the of the list, so the node we inserted becomes the tail of the list.
4. Before a given node
Now we're going to add a new node before we create a list of node. In this case we have node B, then we're going to create list A-C-D. B can be anywhere inside the A-C-D, but we're going tp add B in between A and C so now the list becomes A-B-C-D.
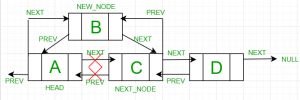
Doubly Linked List | Deletion
Original Doubly Linked List
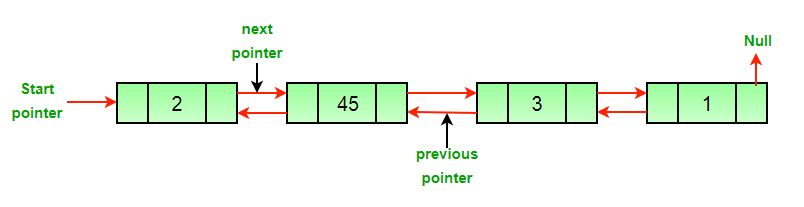
a) After we delete the head of the list
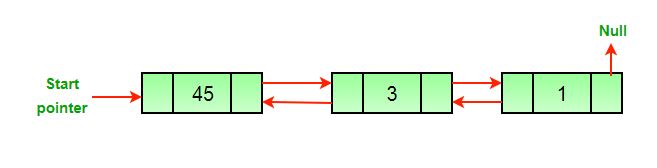
b) After we delete in between nodes of the list
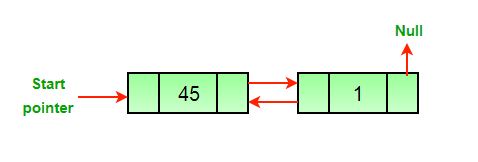
c) After we delete the last node of the list
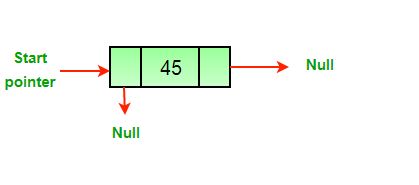
Doubly Circular Linked List | Insertion
1. Insertion at the end of the list or in an empty list
a) Empty List
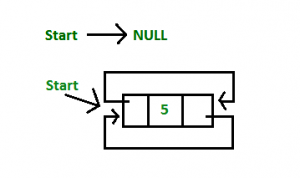
b) At the end of the list
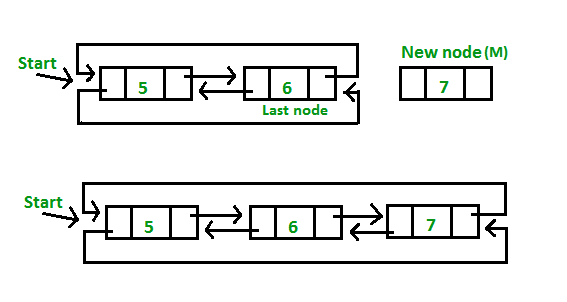
2. Insertion at the beginning of the list
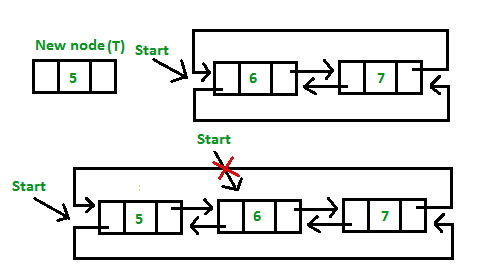
3. Insertion in between the nodes of the list
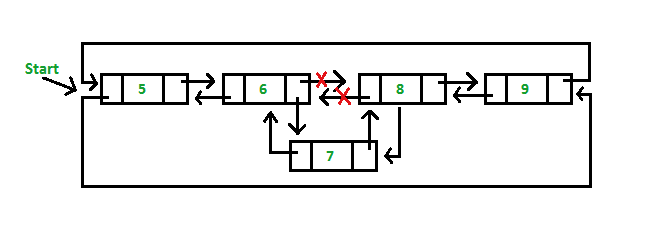
Doubly Circular Linked List | deletion
1. Empty list
Just simply return.
2. List initially contain some nodes, start points to first node of the List
a) Delete the first node of the list
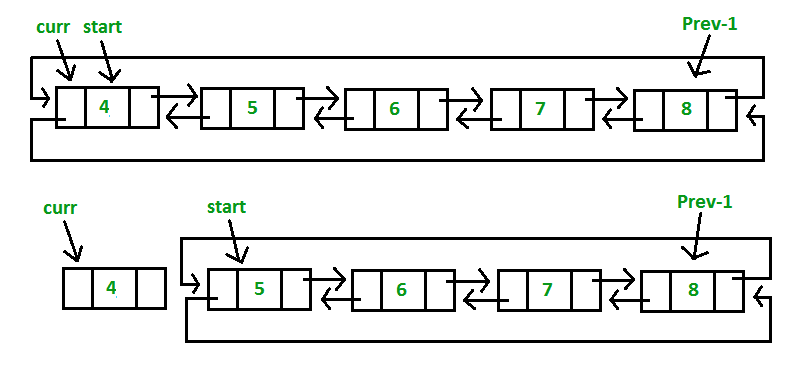
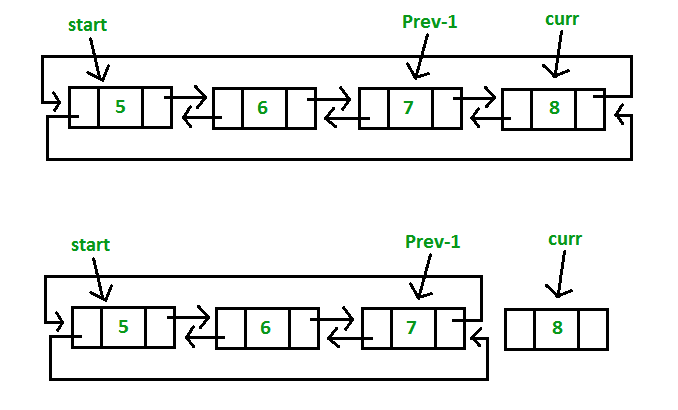
b) Delete the last node of the list
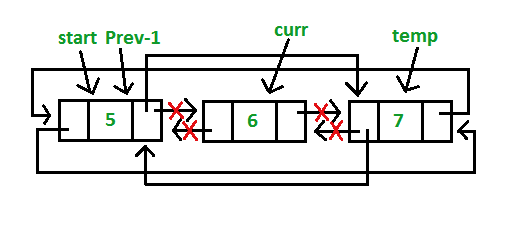
c) Delete in between nodes of the list
references
https://www.geeksforgeeks.org/data-structures/linked-list/https://www.geeksforgeeks.org/circular-singly-linked-list-insertion/https://www.youtube.com/watch?v=njTh_OwMljAhttps://en.wikipedia.org/wiki/Linked_listhttps://visualgo.net/en/list?slide=6